Lake Processing – Raised Cosine Equalization in detail ⁇ IT for AVs ⁇ Bodo Felusch

If you know Lake Processing, you also know the terms Ideal Graphic EQTM and Lake Mesa EQTM. The technology behind it is called Raised Cosine Equalisation. Raised Cosine filters are known from communications technology where they are used to form signal pulses. David McGrath, Justin Baird and Bruce Jackson have used this technique to use logarithmically scaled filter synthesis for lake processing in the Pro Audio range and to improve classic filtering methods. How this works in detail I will describe in the following without getting lost in mathematical equations ...which I don't understand anyway ⁇ The original AES Convention White Paper can be obtained here: http://www.aes.org/e-lib/browse.cfm?elib=12914

Raised Cosine Equalization...why?

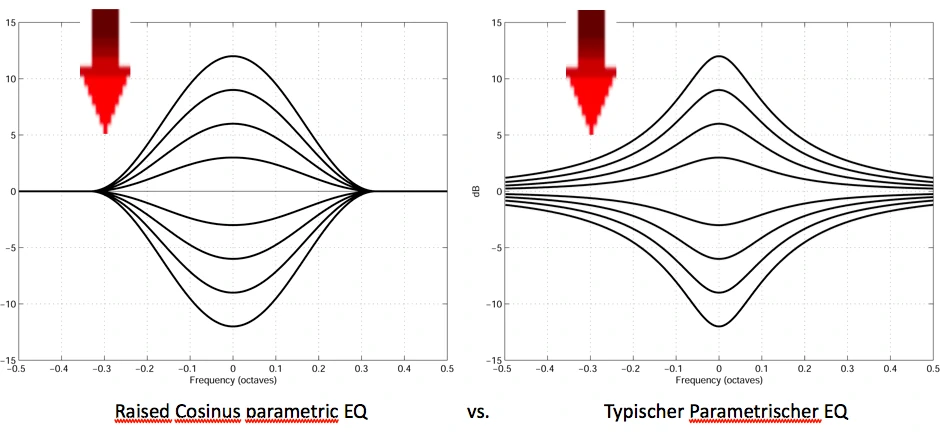
Fig. 1 Comparison of two parametric EQs with third-bandwidth (1/3 Oct) at +6dB gain

Red: typical parametric EQ –> crosstalk to adjacent third bands

Blue: Raised Cosinus EQ -> NO crosstalk in adjacent third bands

Here we see how two filters with identical parameters generate different transmission functions. The "typical" parametric EQ clearly translates into the adjacent third bands at 800Hz and 1250Hz, while the Lake filter does not override based on Raised Cosine calculation.

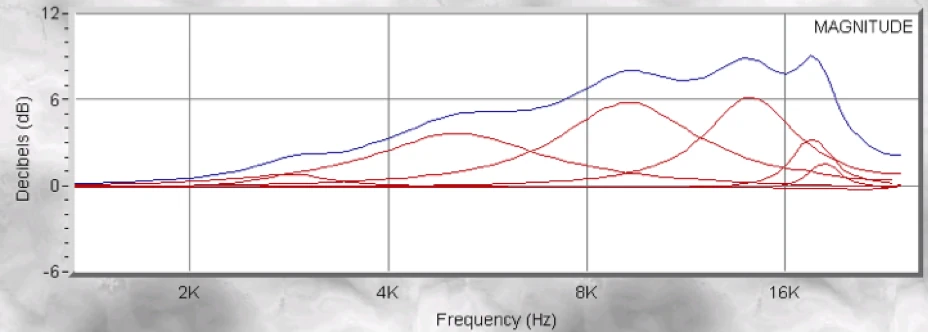
Example of application: Correction of an HF driver

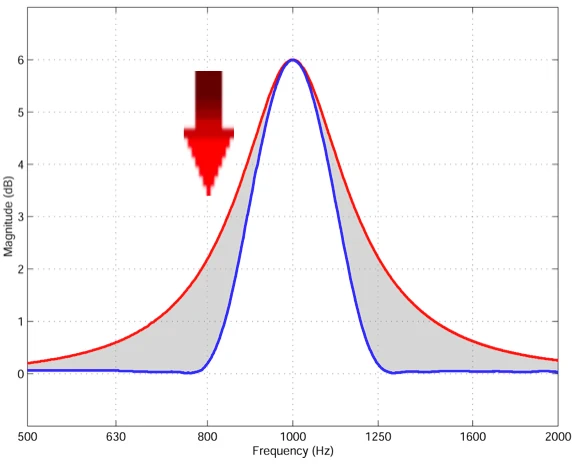
Fig. 2 Typical transmission behaviour of an RF driver

Here we see a typical RF driver ... raw and uncontrolled. How do you correlate this most effectively?

Fig. 3 Correction of the RF driver (blue below) by means of a single Lake MESA filter (blue above). The result is shown in the red curve.

The advantage in this example is that only a single asymmetric filter is needed. Of course, this can also be achieved with “normal” parametric EQs. However, in order to replicate the transmission function of a MESA filter, seven conventional filters are required, which then generate a relatively "wave" frequency and phase response in comparison.

Fig. 4 Replica of a MESA EQ with 7 typical parametric EQs

Disadvantage:

1. Elaborate

2. Inaccurate

You can also recreate the transmission function with a parametric EQ in combination with a high or low pass. However, due to the symmetrical shape, there is always a crosstalk, which means that energy is fed to the driver outside of its transmission range, resulting in distortions and a shorter service life. (especially for subwoofers). High-pass and low-pass filters have a finite slope and just when relatively aprupt transitions into the barrier band are in demand, these can be better realized with asymmetric MESA filters.

Fig. 5 MESA Filter vs. 7 typical parametric EQs

In this way, the transmission range can be corrected without overriding the locking band. Let's say we want to raise 10dB HF and lock at 20kHz with 24dB/oct. Then the LPF would produce -24dB at 40kHz and -12dB at 30kHz. If we now raise by 10dB with a normal PEQ at 20kHz relatively wide, then we would have in the range of 20kHz – 25kHz in combination with the LPF in the best case 0dB, while the MESA in combination with the LPF already lowers 10dB.

Raised Cosine Equalization - What is it?

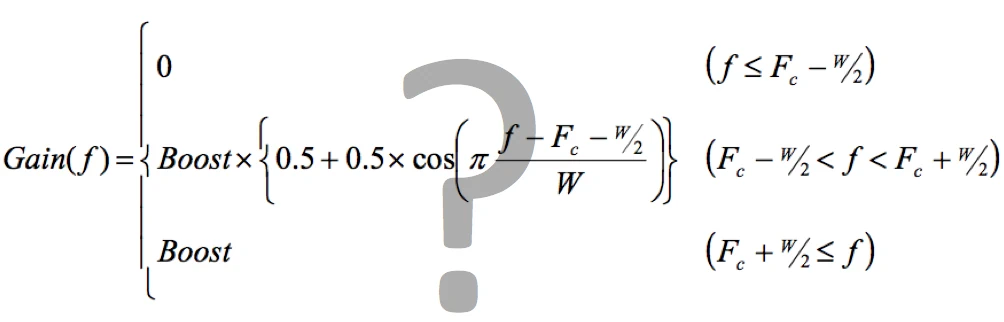
Since the mathematical consideration is not suitable for a better understanding, we now take a path that is more understandable for sound technicians and look at the result of this calculation operation.

Raised Cosinus – Shelf Filter

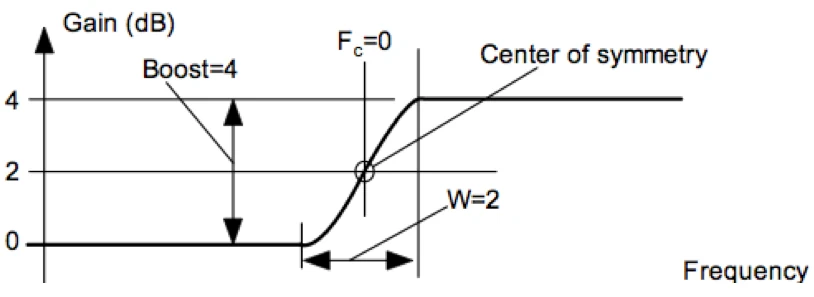
Here we see a Raised Cosinus Shelf Filter. On the frequency axis, linear scaling (Hz) is transformed into a logaritmic (f/octav). Now it is a question of constructing or calculating a transmission curve with certain properties, for this we are looking for computational paths that lead to the following ideal properties as far as possible:

1. very clear transmission band without crosstalk (e.g. 500Hz and 2kHz = 0dB)

2. Possibly even increase (e.g. 0dB @ 500Hz to +4dB @ 2kHz)

3. As continuous a flank as possible (no sharp curves;)

4. As symmetrical as possible (s.h Center of symetry)

The best result can be found in the half-cycle Cosinus function. This is the second word from Raised. Cosine Equalization in naming.

Raised Cosinus - Parametric filter

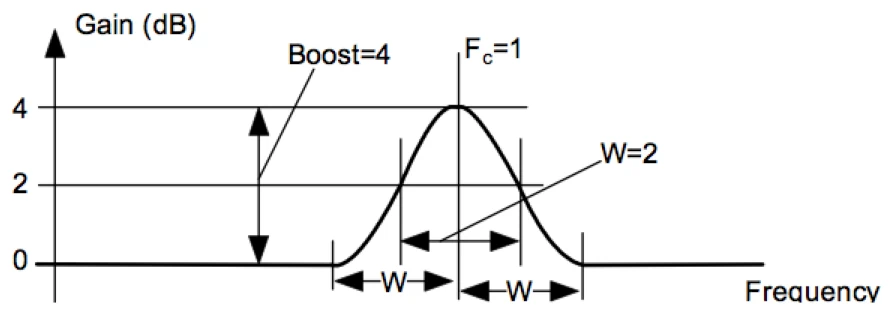
Fig. 8 Transmission function of a Raised Cosinus parametric EQ

A Raised Cosinus parametric EQ consists of two such shelf filters. An ascending (raised) immediately followed by a sloping one. The parametric EQ consists of two shelf filters. Here we find the first word in the naming which stands for the increasing Shelf Filter. Raised Cosinus PEQs have a pure addition behavior to traditional PEQs. Neighbouring bands do not interact with each other unintentionally.

Fig. 9 Comparison of transmission function and crosstalk in neighbouring bands

By linearly summing adjacent filters independently of gain, you need fewer filters for complex transmission functions and benefit from precise frequency and phase responses compared to traditional methods.

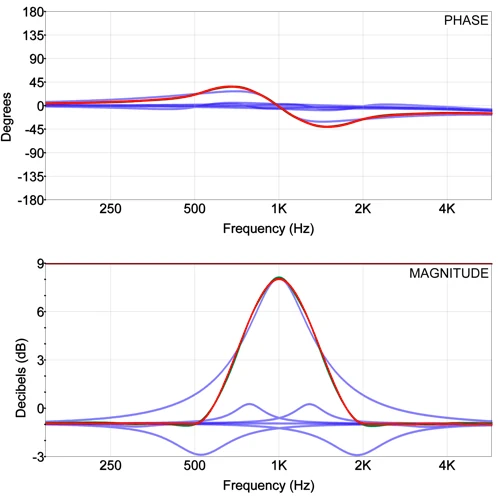
Fig. 10 Replica of a Raised Cosinus param. EQ with 7 conventional param. EQs

The RC-PEQ can also be recreated with 7 conventional PEQs with the same consequences. Roughness in frequency response and phase as described above for the MESA EQ.

Raised Cosine Equalization...what opportunities arise from this?

Lake Mesa EQTM

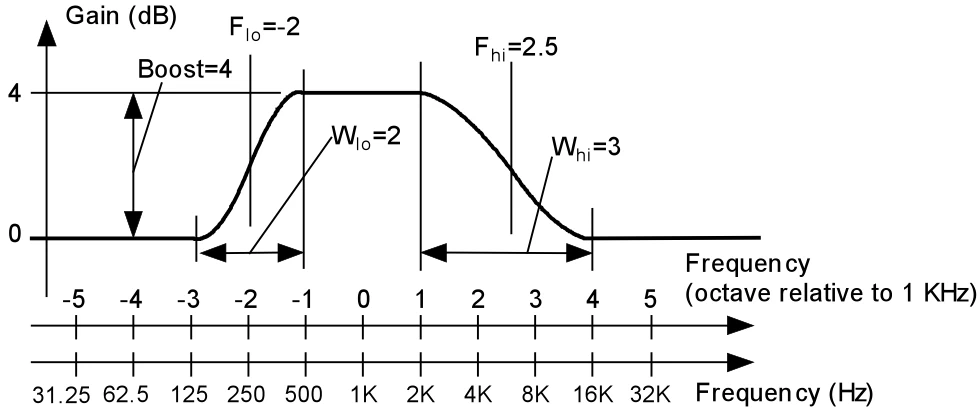
The simple separation of the two combined shelf filters results in an asymmetric MESA filter with separately adjustable slope for the upper and lower cut-off frequency. So we get a perfect tool for the asym. Whether on the manufacturer's side for preset creation or on the user's side for measuring the sound system, the Lake MESA EQ is a simple and intuitive universal weapon.

Complex transmission function, intuitive to use

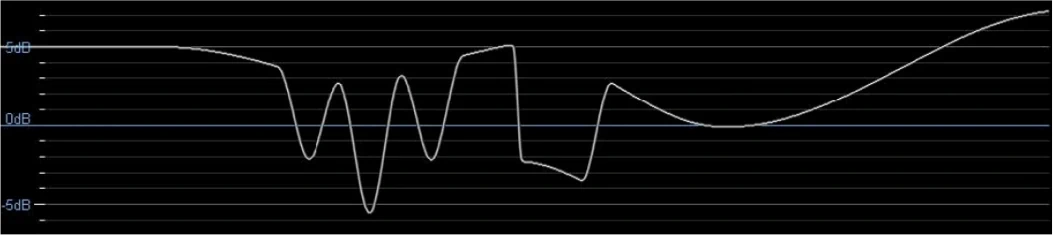
Fig. 12 Example of a resulting filter sum with Lake Processing

The combination of all set filters is shown as the resulting (white) line. The calculation is relatively phase-linear compared to ‘traditional’ methods but not a FIR linear phase filter! This circumstance is further improved by the fact that one comes to the goal with fewer filters. ...e.g. fewer “post-corrections” resulting from the addition of cross-talk PEQs are required.

Ideal Graphic EQTM

Fig. 13 Example of the resulting filter sums with graphic EQs Lake Processing vs. Traditonell

The Raised Cosinus third band filter does not exaggerate into adjacent bands, resulting in the Lake Ideal Graphic EQ a perfect transmission function compared to normal graphic EQs in which individual bands always interact with each other.

advantages

1. Parametric EQ without crosstalk into adjacent bands with pure addition behavior

2. Asymmetric MESA EQ by separating the Shelf Slopes

3. Ideal Graphic EQ since no crosstalk takes place in neighboring third bands

4. Complex transmission functions with intuitive operation.

disadvantages

1. When creating speaker presets, manufacturer information must be converted to PEQs for Lake Processing. However, not in Raised Cosine but in classical biquads, which are however calculated according to a method described by Sophocles J. Orfanidis, which approximates digital filters near the Nyquist frequency better to their analog counterparts. This applies to the output EQs in the Lake module. For this there is an Exeltool which also includes my calculation for Lake Limiter. It can be downloaded here:

Calculation of Lake Limiters & Q to BW Conversion

1 file(s)

662.00 KB

Login

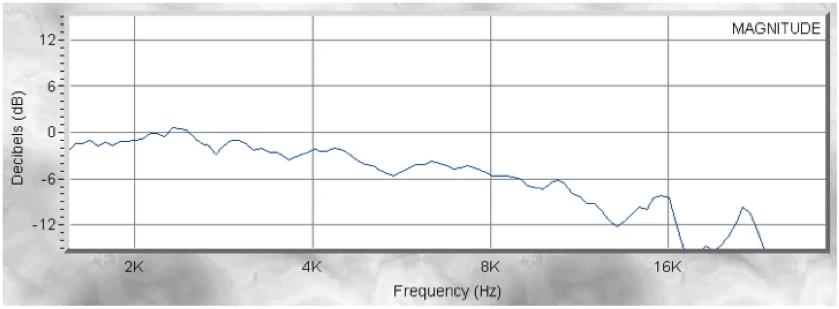
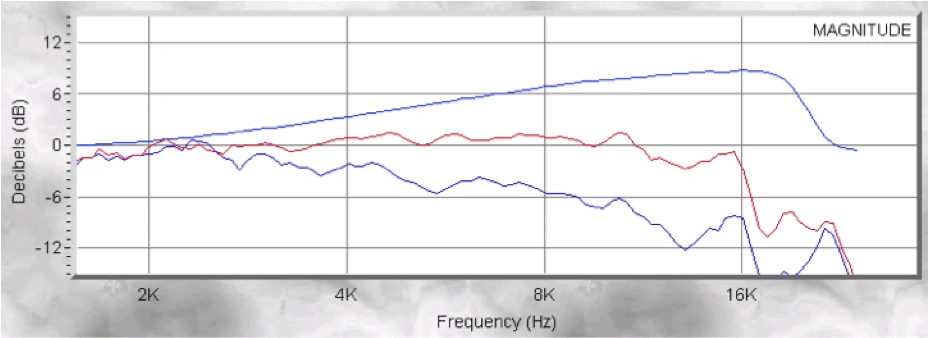
Example of correct conversion

The manufacturer EAW specifies the Q factor and the bandwidth for its loudspeaker JFX260. If you now take the specified bandwidth for the creation of a preset with Lake Processing, which also requires the bandwidth as a parameter, you are acting incorrectly. Using the Exeltool, the specification of the Q factor and gain would be correct to convert to the bandwidth for Lake Processing according to Orfandi's method (in the exemplary filter, a value of 1.9 instead of the specified 1.27 would be correct). What the transmission function of the Lake Processor for the loudspeaker with wrong and correct method looks like we see here.

Fig. 14 Transfer function Lab.gruppen LM44 with EAW JFX260 Processing

The combination of all set filters is shown as the resulting (white) line. The calculation is relatively phase-linear compared to ‘traditional’ methods but not a FIR linear phase filter! This circumstance is further improved by the fact that one comes to the goal with fewer filters. ...e.g. fewer “post-corrections” resulting from the addition of cross-talk PEQs are required.

The red curve shows the original manufacturer's indication of the bandwidth. The green curve shows the correct conversion of the specified Q factor using the Exel tool. By incorrect application of the given manufacturer data, we generate +3.5dB in the range of 2-3kHz ...with an EAW speaker the flat is not exactly the best idea ⁇

conclusion

Raised Cosinus Equalisation is not a witchcraft, you benefit from less interacting PEQs and MESA forms in the Input EQ of the Lake Modules. You only have to be really careful when creating your own speaker presets if manufacturer specifications for Orfandis Biquads in the Lake Output EQ have to be correctly converted. The Lake LoadLibraryTM already includes a number of ready-made presets and is constantly growing. In daily use, you benefit from intuitive EQs with which the most complex transmission functions can be easily and quickly converted, and with very linear phase behavior through more economical use of filters and low latency. If you combine several parametric filters, Raised Cosinus PEQ do not interact negatively with each other as with traditional parametric EQs that cross over into adjacent bands. Since loudspeaker systems in rooms and line arrays of different lengths in particular almost always require asymmetric corrections, the Lake Mesa EQ is the perfect tool to get to your destination quickly and efficiently. This has been so successful for over ten years that the concept has been adopted by other manufacturers. ...Bruce Jackson's idea of building a parametric EQ into a live mixer has prevailed just as much as his idea of making a separate monitor mix or flying speakers ⁇